En posts anteriores vimos cómo crear, entrenar, predecir e incluso evaluar un modelo predictivo. Sin embargo, no cambiamos ninguno de los parámetros del modelo que tenemos a nuestra disposición cuando creamos una instancia. Por ejemplo, para k-nearest neighbors, inicialmente usamos los parámetros por defecto: n_neighbors=5 antes de probar otros parámetros del modelo.
Estos parámetros se denominan hiperparámetros: son parámetros usados para controlar el proceso de aprendizaje, por ejemplo el parámetro k de k-nearest neighbors. Los hiperparámetros son especificados por el usuario, a menudo ajustados manualmente (o por una búsqueda automática exhaustiva) y no pueden ser estimados a partir de los datos. No deben confundirse con los otros parámetros que son inferidos durante el proceso de entrenamiento. Estos parámetros definen el modelo en sí mismo, por ejemplo coef_ para los modelos lineales.
En este post mostraremos en primer lugar que los hiperparámetros tienen un impacto en el rendimiento del modelo y que los valores por defecto no son necesariamente la mejor opción. Posteriormente, mostraremos cómo definir hiperparámetros en un modelo de scikit-learn. Por último, mostraremos estrategias que nos permitirán seleccionar una combinación de hiperparámetros que maximicen el rendimiento del modelo.
En concreto repasaremos los siguientes aspectos:
- cómo usar
get_paramsyset_paramspara obtener los parámetros de un modelo y establecerlos, respectivamente; - cómo optimizar los hiperparámetros de un modelo predictivo a través de grid-search;
- cómo la búsqueda de más de dos hiperparámetros es demasiado costosa;
- cómo grid-search no encuentra necesariamente una solución óptima;
- cómo la búsqueda aleatoria ofrece una buena alternativa a grid-search cuando el número de parámetros a ajustar es más de dos. También evita la regularidad impuesta por grid-search que puede resultar problemática en ocasiones;
- cómo evaluar el rendimiento predictivo de un modelo con hiperparámetros ajustados usando el procedimiento de validación cruzada anidada.
Establecer y obtener hiperparámetros en scikit-learn
El proceso de aprendizaje de un modelo predictivo es conducido por un conjunto de parámetros internos y un conjunto de datos de entrenamiento. Estos parámetros internos se denominan hiperparámetros y son específicos de cada familia de modelos. Además, un conjunto específico de hiperparámetros es óptimo para un dataset específico y, por lo tanto, necesitan optimizarse.
Vamos a mostrar como podemos obtener y establecer el valor de un hiperparámetro en un estimador de scikit-learn. Recordemos que los hiperparámetros se refieren a los parámetros que controlarán el proceso de aprendizaje. No debemos confundirlos con los parámetros entrenados, resultado del entrenamiento. Estos parámetros entrenados se reconocen en scikit-learn porque tienen el sufijo _, por ejemplo, model_coef_.
Utilizaremos el dataset del Censo US de 1944, del que únicamente usaremos las variables numéricas.
import pandas as pd
adult_census = pd.read_csv("adult_census.csv")
target_name = "class"
y = adult_census[target_name]
data = adult_census.drop(columns=[target_name])
numerical_columns = [
"age", "capital-gain", "capital-loss", "hours-per-week"]
X = data[numerical_columns]
X.head()| age | capital-gain | capital-loss | hours-per-week | |
|---|---|---|---|---|
| 0 | 25 | 0 | 0 | 40 |
| 1 | 38 | 0 | 0 | 50 |
| 2 | 28 | 0 | 0 | 40 |
| 3 | 44 | 7688 | 0 | 40 |
| 4 | 18 | 0 | 0 | 30 |
Vamos a crear un modelo predictivo simple compuesto por un scaler seguido por un clasificador de regresión logística.
Muchos modelos, incluidos los lineales, trabajan mejor si todas las características tienen un escalado similar. Para este propósito, usaremos un StandardScaler, que transforma los datos escalando las features.
from sklearn import set_config
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
set_config(display="diagram")
model = Pipeline(steps=[
("preprocessor", StandardScaler()),
("classifier", LogisticRegression())
])Podemos evaluar el rendimiento de generalización del modelo a través de validación cruzada.
from sklearn.model_selection import cross_validate
cv_results = cross_validate(model, X, y)
scores = cv_results["test_score"]
print(f"Puntuación de precisión a través de validación cruzada:\n"
f"{scores.mean():.3f} +/- {scores.std():.3f}")Puntuación de precisión a través de validación cruzada:
0.800 +/- 0.003
Hemos creado un modelo con el valor por defecto de C que es igual a 1. Si quisiéramos usar un parámetro C distinto, podríamos haberlo hecho cuando creamos el objeto LogisticRegression con algo como LogisticRegression(C=1e-3). También podemos cambiar el parámetro de un modelo después de que haya sido creado con el método set_params, disponible para todos los estimadores de scikit-learn. Por ejemplo, podemos establecer C=1e-3, entrenar y evaluar el modelo:
model.set_params(classifier__C=1e-3)
cv_results = cross_validate(model, X, y)
print(f"Puntuación de precisión a través de validación cruzada:\n"
f"{scores.mean():.3f} +/- {scores.std():.3f}")Puntuación de precisión a través de validación cruzada:
0.800 +/- 0.003
Cuando el modelo está en un Pipeline, los nombres de los parámetros tiene la forma <nombre_modelo>__<nombre_parámetro>. En nuestro caso, classifier proviene de la definición del Pipeline y C es el nombre del parámetro de LogisticRegression.
Generalmente, podemos usar el método get_params en los modelos de scikit-learn para listar todos los parámetros con sus respectivos valores.
model.get_params(){'memory': None,
'steps': [('preprocessor', StandardScaler()),
('classifier', LogisticRegression(C=0.001))],
'verbose': False,
'preprocessor': StandardScaler(),
'classifier': LogisticRegression(C=0.001),
'preprocessor__copy': True,
'preprocessor__with_mean': True,
'preprocessor__with_std': True,
'classifier__C': 0.001,
'classifier__class_weight': None,
'classifier__dual': False,
'classifier__fit_intercept': True,
'classifier__intercept_scaling': 1,
'classifier__l1_ratio': None,
'classifier__max_iter': 100,
'classifier__multi_class': 'auto',
'classifier__n_jobs': None,
'classifier__penalty': 'l2',
'classifier__random_state': None,
'classifier__solver': 'lbfgs',
'classifier__tol': 0.0001,
'classifier__verbose': 0,
'classifier__warm_start': False}
get_params devuelve un diccionario cuyas claves son los nombres de los parámetros y sus valores los valores de dichos parámetros. Si queremos obtener el valor de un único parámetro, por ejemplo, classifier__C usamos lo siguiente:
model.get_params()["classifier__C"]0.001
Podemos variar sistemáticamente el valor de C para ver si existe un valor óptimo.
for C in [1e-3, 1e-2, 1e-1, 1, 10]:
model.set_params(classifier__C=C)
cv_results = cross_validate(model, X, y)
scores = cv_results["test_score"]
print(f"Puntuación de precisión de validación cruzada con C={C}:\n"
f"{scores.mean():.3f} +/- {scores.std():.3f}")Puntuación de precisión de validación cruzada con C=0.001:
0.787 +/- 0.002
Puntuación de precisión de validación cruzada con C=0.01:
0.799 +/- 0.003
Puntuación de precisión de validación cruzada con C=0.1:
0.800 +/- 0.003
Puntuación de precisión de validación cruzada con C=1:
0.800 +/- 0.003
Puntuación de precisión de validación cruzada con C=10:
0.800 +/- 0.003
Podemos ver que mientras C sea lo suficientemente alto, el modelo parece rendir bien.
Lo que hemos hecho aquí es muy manual: implica recorrer los valores de C y seleccionar manualmente el mejor. Veremos cómo realizar esta tarea de forma automática.
Cuando evaluamos una familia de modelos en datos de prueba y seleccionamos el que mejor se ejecuta, no podemos confiar en la correpondiente precisión de la estimación y necesitamos aplicar el modelo en nuevos datos. De hecho, los datos de prueba se han usado para seleccionar el modelo y, por lo tanto, ya no es independiente de este modelo.
Ajuste de hiperparámetros por grid-search
Vamos a mostrar cómo optimizar hiperparámetros usando el enfoque de grid-search.
Seguimos con nuestro dataset del censo.
target_name = "class"
y = adult_census[target_name]
y.head()0 <=50K
1 <=50K
2 >50K
3 >50K
4 <=50K
Name: class, dtype: object
Vamos a eliminar de nuestro datos el objetivo y la columna "education-num", dado que es información duplicada de la columna "education".
X = adult_census.drop(columns=[target_name, "education-num"])
X.head()| age | workclass | fnlwgt | education | marital-status | occupation | relationship | race | sex | capital-gain | capital-loss | hours-per-week | native-country | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 25 | Private | 226802 | 11th | Never-married | Machine-op-inspct | Own-child | Black | Male | 0 | 0 | 40 | United-States |
| 1 | 38 | Private | 89814 | HS-grad | Married-civ-spouse | Farming-fishing | Husband | White | Male | 0 | 0 | 50 | United-States |
| 2 | 28 | Local-gov | 336951 | Assoc-acdm | Married-civ-spouse | Protective-serv | Husband | White | Male | 0 | 0 | 40 | United-States |
| 3 | 44 | Private | 160323 | Some-college | Married-civ-spouse | Machine-op-inspct | Husband | Black | Male | 7688 | 0 | 40 | United-States |
| 4 | 18 | ? | 103497 | Some-college | Never-married | ? | Own-child | White | Female | 0 | 0 | 30 | United-States |
Dividimos el dataset en entrenamiento y prueba.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)Vamos a definir un pipeline y manejaremos tanto las variables numéricas como las categóricas.
from sklearn.compose import make_column_selector as selector
categorical_columns_selector = selector(dtype_include=object)
categorical_columns = categorical_columns_selector(X)En este caso, estamos usando un modelo basado en árbol como un clasificador (es decir, HistGradientBoostingClassifier). Esto significa que:
- las variables numéricas no necesitan escalado;
- las variables categóricas se pueden manejar con un
OrdinalEncoderincluso si el orden codificado no tiene sentido; - En los modelos basados en árbol,
OrdinalEncoderevita tener representaciones de alta dimensionalidad.
Vamos a construir nuestro OrdinalEncoder pasándole las categorías conocidas.
from sklearn.preprocessing import OrdinalEncoder
categorical_preprocessor = OrdinalEncoder(handle_unknown="use_encoded_value",
unknown_value=-1)Usaremos un ColumnTransformer para seleccionar las columnas categóricas y aplicarles el OrdinalEncoder.
from sklearn.compose import ColumnTransformer
preprocessor = ColumnTransformer([
("cat_preprocessor", categorical_preprocessor, categorical_columns)],
remainder="passthrough", sparse_threshold=0)Por último, usaremos un clasificador de árbol (por ejemplo, histogram gradient-boosting) para predecir si una persona gana más de 50 k$ al año.
from sklearn.ensemble import HistGradientBoostingClassifier
model = Pipeline([
("preprocessor", preprocessor),
("classifier", HistGradientBoostingClassifier(
random_state=42, max_leaf_nodes=4
))
])
modelPipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1), ['workclass', 'education','marital-status','occupation', 'relationship','race', 'sex','native-country'])])),('classifier',HistGradientBoostingClassifier(max_leaf_nodes=4,random_state=42))])Please rerun this cell to show the HTML repr or trust the notebook.Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education','marital-status','occupation', 'relationship','race', 'sex','native-country'])])),('classifier',HistGradientBoostingClassifier(max_leaf_nodes=4,random_state=42))])ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education', 'marital-status','occupation', 'relationship', 'race', 'sex','native-country'])])['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']
OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=-1)
passthrough
HistGradientBoostingClassifier(max_leaf_nodes=4, random_state=42)
Pasemos ahora al ajuste con grid-search. Anteriormente usamos un bucle for para cada hiperparámetro con el fin de encontrar la mejor combinación a partir de un conjunto de valores. La clase GridSearchCV de scikit-learn implementa una lógica muy similar con mucho menos código repetitivo. Vamos a ver cómo usar el estimador GridSearchCV para realizar esta búsqueda. Dado que grid-search puede ser costoso, únicamente exploraremos la combinación tasa de aprendizaje y máximo número de nodos.
%%time
from sklearn.model_selection import GridSearchCV
param_grid = {
"classifier__learning_rate": (0.01, 0.1, 1, 10),
"classifier__max_leaf_nodes": (3, 10, 30)}
model_grid_search = GridSearchCV(model, param_grid=param_grid,
n_jobs=-1, cv=2)
model_grid_search.fit(X_train, y_train)CPU times: total: 14.3 s
Wall time: 5.51 s
GridSearchCV(cv=2,estimator=Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough',sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass','education','marital-status','occupation','relationship','race','sex','native-country'])])),('classifier',HistGradientBoostingClassifier(max_leaf_nodes=4,random_state=42))]),n_jobs=-1,param_grid={'classifier__learning_rate': (0.01, 0.1, 1, 10),'classifier__max_leaf_nodes': (3, 10, 30)})Please rerun this cell to show the HTML repr or trust the notebook.GridSearchCV(cv=2,estimator=Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough',sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass','education','marital-status','occupation','relationship','race','sex','native-country'])])),('classifier',HistGradientBoostingClassifier(max_leaf_nodes=4,random_state=42))]),n_jobs=-1,param_grid={'classifier__learning_rate': (0.01, 0.1, 1, 10),'classifier__max_leaf_nodes': (3, 10, 30)})ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education', 'marital-status','occupation', 'relationship', 'race', 'sex','native-country'])])['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']
OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=-1)
passthrough
HistGradientBoostingClassifier(max_leaf_nodes=4, random_state=42)
Finalmente, comprobamos la precisión de nuestro modelo usando el conjunto de prueba.
accuracy = model_grid_search.score(X_test, y_test)
print(f"La puntuación de precisión de prueba del pipeline grid-search es:"
f"{accuracy:.2f}")La puntuación de precisión de prueba del pipeline grid-search es:0.88
El estimador GridSearchCV toma una parámetro param_grid que define todos los hiperparámetros y sus valores asociados. Grid-search se encargará de crear todas las posibles combinaciones y probarlas.
El número de combinaciones será igual al producto del número de valores a explorar para cada parámetros (es decir, en nuestro ejemplo 4 x 3 combinaciones). Por tanto, añadir nuevos parámetros con sus valores asociados a ser explorados se vuelve rápidamente computacionalmente costoso.
Una vez que grid-search es entrenado, se puede usar como cualquier otro predictor llamando a sus métodos predict y predict_proba. Internamente, usará el modelo con los mejores parámetros encontrados durante el fit.
Vamos a obtener las predicciones para los primeros 5 ejemplos usando el estimador con los mejores parámetros.
model_grid_search.predict(X_test.iloc[0:5])array([' <=50K', ' <=50K', ' >50K', ' <=50K', ' >50K'], dtype=object)
Podemos conocer cuáles son esos parámetros mirando el atributo best_params_.
model_grid_search.best_params_{'classifier__learning_rate': 0.1, 'classifier__max_leaf_nodes': 30}
La precisión y los mejores parámetros del pipeline de grid-search son similares a los que encontramos anteriormente, donde localizamos los mejores parámetros “a mano” usando un doble bucle for. Además, podemos inspeccionar todos los resultados, los cuales se almacenan en el atributo cv_results_ de grid-search. Filtraremos algunas columnas específicas de estos resultados.
cv_results = pd.DataFrame(model_grid_search.cv_results_).sort_values(
"mean_test_score", ascending=False)
cv_results.head()| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_classifier__learning_rate | param_classifier__max_leaf_nodes | params | split0_test_score | split1_test_score | mean_test_score | std_test_score | rank_test_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 1.032387 | 4.768372e-07 | 0.214684 | 0.006005 | 0.1 | 30 | {'classifier__learning_rate': 0.1, 'classifier... | 0.867766 | 0.867649 | 0.867708 | 0.000058 | 1 |
| 4 | 0.762404 | 4.478788e-02 | 0.288248 | 0.020517 | 0.1 | 10 | {'classifier__learning_rate': 0.1, 'classifier... | 0.866729 | 0.866557 | 0.866643 | 0.000086 | 2 |
| 6 | 0.374071 | 4.829156e-02 | 0.169396 | 0.021768 | 1 | 3 | {'classifier__learning_rate': 1, 'classifier__... | 0.860559 | 0.861261 | 0.860910 | 0.000351 | 3 |
| 7 | 0.241707 | 8.007050e-03 | 0.133865 | 0.009759 | 1 | 10 | {'classifier__learning_rate': 1, 'classifier__... | 0.857993 | 0.861862 | 0.859927 | 0.001934 | 4 |
| 3 | 0.545218 | 5.529642e-02 | 0.250966 | 0.017766 | 0.1 | 3 | {'classifier__learning_rate': 0.1, 'classifier... | 0.852752 | 0.854272 | 0.853512 | 0.000760 | 5 |
Con solo dos parámetros podriamos visualizar el grid-search con un mapa de calor. Necesitamos transformar nuestro cv_results en un dataframe donde:
- las filas corresponderán a los valores de la tasa de aprendizaje;
- las columnas corresponderán al mnúmero máximo de hojas;
- el contenido del dataframe serán las puntuaciones de prueba medias.
pivoted_cv_results = cv_results.pivot_table(
values="mean_test_score", index=['param_classifier__learning_rate'],
columns=["param_classifier__max_leaf_nodes"])
pivoted_cv_results| param_classifier__max_leaf_nodes | 3 | 10 | 30 |
|---|---|---|---|
| param_classifier__learning_rate | |||
| 0.01 | 0.797166 | 0.817832 | 0.845541 |
| 0.10 | 0.853512 | 0.866643 | 0.867708 |
| 1.00 | 0.860910 | 0.859927 | 0.851547 |
| 10.00 | 0.283476 | 0.618080 | 0.351642 |
Podemos usa una representación de mapa de calor para mostrar visualmente el dataframe anterior.
import seaborn as sns
ax = sns.heatmap(pivoted_cv_results, annot=True, cmap="YlGnBu", vmin=0.7,
vmax=0.9)
ax.invert_yaxis()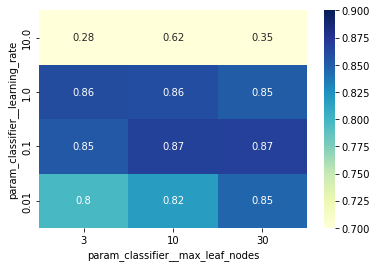
Observando el mapa de calor podemos resaltar algunas cosas:
- Para valores muy altos de
learning_rate, el rendimiento de generalización del modelo se degrada y ajustar el valor demax_leaf_nodesno arregla el problema; - fuera de esta región problemática, observamos que la opción óptima de
max_leaf_nodesdepende del valor delearning_rate; - en particular, observamos una “diagonal” de buenos modelos con una precisión cercana al máximo de 0.87: cuando el valor de
max_leaf_nodesse incrementa, debemos disminuir el valor delearning_rateacordemente para mantener una buena precisión.
Por ahora, tengamos en cuenta que, en general, no existe una única configuración óptima de parámetros: 4 modelos de las 12 configuraciones de parámetros alcanzan la máxima precisión (hasta pequeñas fluctuaciones aleatorias causadas por el muestreo del conjunto de entrenamiento).
Ajuste de hiperparámetros por randomized-search
Hemos visto que el enfoque de grid-search tiene sus limitaciones. No escala cuando el número de parámetros a ajustar aumenta. Además, grid-search impone una regularidad durante la búsqueda que podría ser problemática. Vamos a presentar otro método para ajustar hiperparámetros denominado búsqueda aleatoria.
Partimos del mismo dataset, el cual hemos dividido en entrenamiento y prueba, y hemos realizado el mismo pipeline de preprocesado.
modelPipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough',sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education','marital-status','occupation', 'relationship','race', 'sex','native-country'])])),('classifier',HistGradientBoostingClassifier(max_leaf_nodes=4,random_state=42))])Please rerun this cell to show the HTML repr or trust the notebook.Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education','marital-status','occupation', 'relationship','race', 'sex','native-country'])])),('classifier',HistGradientBoostingClassifier(max_leaf_nodes=4,random_state=42))])ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education', 'marital-status','occupation', 'relationship', 'race', 'sex','native-country'])])['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']
OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=-1)
passthrough
HistGradientBoostingClassifier(max_leaf_nodes=4, random_state=42)
Con el estimador GridSearchCV, los parámetros necesitan ser explicitamente especificados. Ya mencionamos que explorar un gran número de valores para diferentes valores sería rápidamente intratable. En su lugar, podemos generar aleatoriamente parámetros candidatos. De hecho, este enfoque evita la regularidad de grid-search. Por tanto, agregar más evaluaciones puede aumentar la resolución en cada dirección. Este es el caso de la frecuente situación en la que la elección de algunos hiperparámetros no es muy importante, como ocurre con el hiperparámetro 2 del siguiente diagrama.
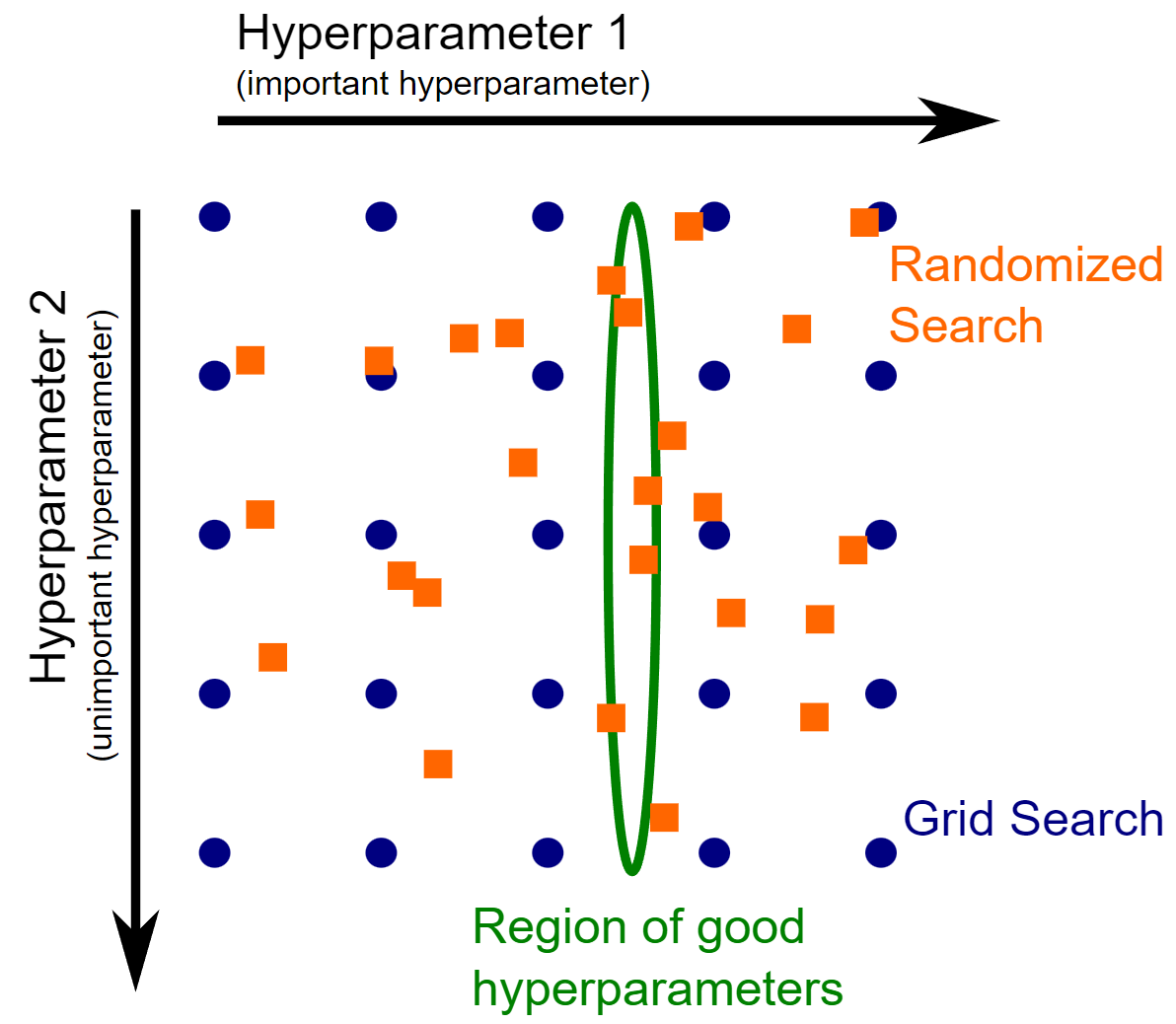
De hecho, el número de puntos de evaluación debe ser dividido entre los dos diferentes hiperparámetros. Con un grid-search, el peligro es que esta región de buenos hiperparámetros quede entre la línea del grid: esta región está alineada con el grid dado que el hiperparámetro 2 tiene una influencia débil. Por contra, la búsqueda estocástica muestreará el hiperparámetro 1 independientemente del hiperparámetro 2 y buscará la región óptima.
La clase RandomizedSearchCV permite esta búsqueda estocástica. Se usa de forma similar a GridSearchCV pero se necesitan especificar las distribuciones de muestreo en lugar de los valores de los parámetros. Por ejemplo, dibujaremos candidatos usando una distribución logarítmica uniforme porque los parámetros que nos interesan toman valores posivos con una escala logarítmica natural (.1 es tan cercano a 1 como éste lo es a 10).
Normalmente, para optimizar 3 o más hiperparámetros, la búsqueda aleatoria es más beneficiosa que grid-search.
Optimizaremos otros 3 parámetros además de los que ya optimizamos con grid-search:
l2_regularization: corresponde con la fortaleza de la regularización;min_samples_leaf: corresponde con el número mínimo de muestras requerida en una hoja;max_bins: corresponde con el número máximo de contenedores para construir histogramas.
Podemos usar scipy.stats.loguniform para generar números flotantes. Para generar valores aleatorios para parámetros con valores enteros (por ejemplo, min_samples_leaf) podemos adaptarlo como sigue:
from scipy.stats import loguniform
class loguniform_int:
"""versión para valores enteror de la distribución log-uniform"""
def __init__(self, a, b):
self._distribution = loguniform(a, b)
def rvs(self, *args, **kwargs):
"""Ejemplo de variable aleatoria"""
return self._distribution.rvs(*args, **kwargs).astype(int)Ahora podemos definir la búsqueda aleatoria usando diferentes distribuciones. Ejecutar 10 iteraciones de 5-particiones de validación cruzada para parametrizaciones aleatorias de este modelo en este dataset puede llevar desde 10 segundos a varios minutos, dependiendo de la velocidad de la máquina y del número de procesadores disponibles.
%%time
from sklearn.model_selection import RandomizedSearchCV
param_distributions = {
'classifier__l2_regularization': loguniform(1e-6, 1e3),
'classifier__learning_rate': loguniform(0.001, 10),
'classifier__max_leaf_nodes': loguniform_int(2, 256),
'classifier__min_samples_leaf': loguniform_int(1, 100),
'classifier__max_bins': loguniform_int(2, 255),
}
model_random_search = RandomizedSearchCV(
model, param_distributions=param_distributions, n_iter=10,
cv=5, verbose=1, n_jobs=-1
)
model_random_search.fit(X_train, y_train)Fitting 5 folds for each of 10 candidates, totalling 50 fits
CPU times: total: 4.31 s
Wall time: 7.23 s
RandomizedSearchCV(cv=5,estimator=Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough',sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass','education','marital-status','occupation','relationship','race','sex','native-country'])])),('classifier',Hi...'classifier__learning_rate': <scipy.stats._distn_infrastructure.rv_frozen object at 0x0000023201C853F0>,'classifier__max_bins': <__main__.loguniform_int object at 0x0000023201C86110>,'classifier__max_leaf_nodes': <__main__.loguniform_int object at 0x0000023201C86020>,'classifier__min_samples_leaf': <__main__.loguniform_int object at 0x0000023201C844F0>},verbose=1)Please rerun this cell to show the HTML repr or trust the notebook.RandomizedSearchCV(cv=5,estimator=Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough',sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass','education','marital-status','occupation','relationship','race','sex','native-country'])])),('classifier',Hi...'classifier__learning_rate': <scipy.stats._distn_infrastructure.rv_frozen object at 0x0000023201C853F0>,'classifier__max_bins': <__main__.loguniform_int object at 0x0000023201C86110>,'classifier__max_leaf_nodes': <__main__.loguniform_int object at 0x0000023201C86020>,'classifier__min_samples_leaf': <__main__.loguniform_int object at 0x0000023201C844F0>},verbose=1)ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education', 'marital-status','occupation', 'relationship', 'race', 'sex','native-country'])])['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']
OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=-1)
passthrough
HistGradientBoostingClassifier(max_leaf_nodes=4, random_state=42)
Después podemos calcular la puntuación de precisión en el conjunto de prueba.
accuracy = model_random_search.score(X_test, y_test)
print(f"La puntuación de precisión de prueba del mejor modelo es:"
f"{accuracy:.2f}")La puntuación de precisión de prueba del mejor modelo es:0.87
model_random_search.best_params_{'classifier__l2_regularization': 0.0006474800575651534,
'classifier__learning_rate': 0.9584980078111938,
'classifier__max_bins': 131,
'classifier__max_leaf_nodes': 23,
'classifier__min_samples_leaf': 98}
Como ya vimos, podemos inspeccionar los resultados usando el atributo cv_results.
cv_results| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_classifier__learning_rate | param_classifier__max_leaf_nodes | params | split0_test_score | split1_test_score | mean_test_score | std_test_score | rank_test_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 1.032387 | 4.768372e-07 | 0.214684 | 0.006005 | 0.1 | 30 | {'classifier__learning_rate': 0.1, 'classifier... | 0.867766 | 0.867649 | 0.867708 | 0.000058 | 1 |
| 4 | 0.762404 | 4.478788e-02 | 0.288248 | 0.020517 | 0.1 | 10 | {'classifier__learning_rate': 0.1, 'classifier... | 0.866729 | 0.866557 | 0.866643 | 0.000086 | 2 |
| 6 | 0.374071 | 4.829156e-02 | 0.169396 | 0.021768 | 1 | 3 | {'classifier__learning_rate': 1, 'classifier__... | 0.860559 | 0.861261 | 0.860910 | 0.000351 | 3 |
| 7 | 0.241707 | 8.007050e-03 | 0.133865 | 0.009759 | 1 | 10 | {'classifier__learning_rate': 1, 'classifier__... | 0.857993 | 0.861862 | 0.859927 | 0.001934 | 4 |
| 3 | 0.545218 | 5.529642e-02 | 0.250966 | 0.017766 | 0.1 | 3 | {'classifier__learning_rate': 0.1, 'classifier... | 0.852752 | 0.854272 | 0.853512 | 0.000760 | 5 |
| 8 | 0.309014 | 1.376224e-02 | 0.131613 | 0.006506 | 1 | 30 | {'classifier__learning_rate': 1, 'classifier__... | 0.849749 | 0.853344 | 0.851547 | 0.001798 | 6 |
| 2 | 1.302117 | 5.504763e-02 | 0.221190 | 0.011009 | 0.01 | 30 | {'classifier__learning_rate': 0.01, 'classifie... | 0.843252 | 0.847830 | 0.845541 | 0.002289 | 7 |
| 1 | 0.884009 | 4.879224e-02 | 0.331785 | 0.014512 | 0.01 | 10 | {'classifier__learning_rate': 0.01, 'classifie... | 0.818956 | 0.816708 | 0.817832 | 0.001124 | 8 |
| 0 | 0.568239 | 5.479753e-02 | 0.272483 | 0.028774 | 0.01 | 3 | {'classifier__learning_rate': 0.01, 'classifie... | 0.797882 | 0.796451 | 0.797166 | 0.000715 | 9 |
| 10 | 0.200672 | 2.001750e-02 | 0.090077 | 0.011010 | 10 | 10 | {'classifier__learning_rate': 10, 'classifier_... | 0.742356 | 0.493803 | 0.618080 | 0.124277 | 10 |
| 11 | 0.177403 | 1.376188e-02 | 0.084322 | 0.009258 | 10 | 30 | {'classifier__learning_rate': 10, 'classifier_... | 0.364545 | 0.338739 | 0.351642 | 0.012903 | 11 |
| 9 | 0.214183 | 5.004406e-03 | 0.123356 | 0.020768 | 10 | 3 | {'classifier__learning_rate': 10, 'classifier_... | 0.279701 | 0.287251 | 0.283476 | 0.003775 | 12 |
Tengamos en mente que este ajuste está limitado por el número de combinaciones diferentes de parámetros que se puntúan mediante búsqueda aleatoria. De hecho, puede haber otros conjuntos de parámetros que conduzcan a un similar o mejor rendimiento de generalización pero que no hayan sido probados en la búsqueda. En la práctica, la búsqueda aleatoria de hiperparámetros se ejecuta con un gran número de iteraciones. Para evitar el coste computacional y aun así realizar un análisis decente, cargamos los resultados obtenidos de una búsqueda similar con 200 iteraciones.
%%time
model_random_search = RandomizedSearchCV(
model, param_distributions=param_distributions, n_iter=200,
cv=5, verbose=1, n_jobs=-1
)
model_random_search.fit(X_train, y_train)Fitting 5 folds for each of 200 candidates, totalling 1000 fits
CPU times: total: 39.7 s
Wall time: 1min 28s
RandomizedSearchCV(cv=5,estimator=Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough',sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass','education','marital-status','occupation','relationship','race','sex','native-country'])])),('classifier',Hi...'classifier__learning_rate': <scipy.stats._distn_infrastructure.rv_frozen object at 0x0000023201C853F0>,'classifier__max_bins': <__main__.loguniform_int object at 0x0000023201C86110>,'classifier__max_leaf_nodes': <__main__.loguniform_int object at 0x0000023201C86020>,'classifier__min_samples_leaf': <__main__.loguniform_int object at 0x0000023201C844F0>},verbose=1)Please rerun this cell to show the HTML repr or trust the notebook.RandomizedSearchCV(cv=5,estimator=Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough',sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass','education','marital-status','occupation','relationship','race','sex','native-country'])])),('classifier',Hi...'classifier__learning_rate': <scipy.stats._distn_infrastructure.rv_frozen object at 0x0000023201C853F0>,'classifier__max_bins': <__main__.loguniform_int object at 0x0000023201C86110>,'classifier__max_leaf_nodes': <__main__.loguniform_int object at 0x0000023201C86020>,'classifier__min_samples_leaf': <__main__.loguniform_int object at 0x0000023201C844F0>},verbose=1)ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education', 'marital-status','occupation', 'relationship', 'race', 'sex','native-country'])])['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']
OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=-1)
passthrough
HistGradientBoostingClassifier(max_leaf_nodes=4, random_state=42)
accuracy = model_random_search.score(X_test, y_test)
print(f"La puntuación de precisión de prueba del mejor modelo es: "
f"{accuracy:.2f}")La puntuación de precisión de prueba del mejor modelo es: 0.88
def shorten_param(param_name):
if "__" in param_name:
return param_name.rsplit("__", 1)[1]
return param_namecv_results = pd.DataFrame(model_random_search.cv_results_).sort_values(
"mean_test_score", ascending=False)
cv_results = cv_results.rename(shorten_param, axis=1)
cv_results.head()| mean_fit_time | std_fit_time | mean_score_time | std_score_time | l2_regularization | learning_rate | max_bins | max_leaf_nodes | min_samples_leaf | params | split0_test_score | split1_test_score | split2_test_score | split3_test_score | split4_test_score | mean_test_score | std_test_score | rank_test_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 13 | 1.229856 | 0.098360 | 0.121906 | 0.002678 | 0.947496 | 0.126528 | 173 | 21 | 3 | {'classifier__l2_regularization': 0.9474964020... | 0.868705 | 0.872782 | 0.873191 | 0.866912 | 0.870325 | 0.870383 | 0.002388 | 1 |
| 186 | 1.809153 | 0.109481 | 0.156434 | 0.003111 | 6.955393 | 0.136036 | 168 | 32 | 1 | {'classifier__l2_regularization': 6.9553925685... | 0.867886 | 0.872236 | 0.871007 | 0.867731 | 0.871690 | 0.870110 | 0.001920 | 2 |
| 195 | 1.138879 | 0.130649 | 0.128410 | 0.010519 | 16.334498 | 0.25793 | 252 | 16 | 4 | {'classifier__l2_regularization': 16.334498052... | 0.868978 | 0.872372 | 0.870461 | 0.864728 | 0.871963 | 0.869701 | 0.002760 | 3 |
| 47 | 1.520606 | 0.067083 | 0.144124 | 0.011037 | 0.253969 | 0.040045 | 138 | 28 | 8 | {'classifier__l2_regularization': 0.2539688800... | 0.866112 | 0.871553 | 0.869915 | 0.865684 | 0.868960 | 0.868445 | 0.002243 | 4 |
| 98 | 0.409552 | 0.040553 | 0.064756 | 0.010694 | 0.000011 | 0.955962 | 222 | 5 | 4 | {'classifier__l2_regularization': 1.1497260106... | 0.860516 | 0.870598 | 0.868823 | 0.866230 | 0.864182 | 0.866070 | 0.003536 | 5 |
Como tenemos más de 2 parámetros en nuestra búsqueda aleatoria no podemos visualizar los resultados con un mapa de calor. Aún podríamos hacerlo por parejas, pero tener una proyección bidimensional de un problema multidimensional nos puede conducir a una interpresación errónea de las puntuaciones.
import numpy as np
df = pd.DataFrame(
{
"max_leaf_nodes": cv_results["max_leaf_nodes"],
"learning_rate": cv_results["learning_rate"],
"score_bin": pd.cut(
cv_results["mean_test_score"], bins=np.linspace(0.5, 1.0, 6)
),
}
)
sns.set_palette("YlGnBu_r")
ax = sns.scatterplot(
data=df,
x="max_leaf_nodes",
y="learning_rate",
hue="score_bin",
s=50,
color="k",
edgecolor=None,
)
ax.set_xscale("log")
ax.set_yscale("log")
_ = ax.legend(title="mean_test_score", loc="center left", bbox_to_anchor=(1, 0.5))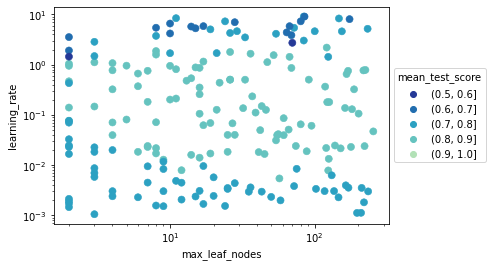
En el gráfico podemos ver que las mejores ejecuciones se encuentran en un rango de tasa de aprendizaje de entre 0.01 y 1.0, pero no tenemos control sobre cómo interactúan los otros hiperparámetros en la tasa de aprendizaje. En su lugar, podemos visualizar todos los hiperparámetros al mismo tiempo usando un gráfico de coordenadas paralelas.
cv_results["l2_regularization"] = cv_results["l2_regularization"].astype("float64")
cv_results["learning_rate"] = cv_results["learning_rate"].astype("float64")
cv_results["max_bins"] = cv_results["max_bins"].astype("float64")
cv_results["max_leaf_nodes"] = cv_results["max_leaf_nodes"].astype("float64")
cv_results["min_samples_leaf"] = cv_results["min_samples_leaf"].astype("float64")import plotly.express as px
fig = px.parallel_coordinates(
cv_results.rename(shorten_param, axis=1).apply(
{
"learning_rate": np.log10,
"max_leaf_nodes": np.log2,
"max_bins": np.log2,
"min_samples_leaf": np.log10,
"l2_regularization": np.log10,
"mean_test_score": lambda x: x,
}
),
color="mean_test_score",
color_continuous_scale=px.colors.sequential.Viridis,
)
fig.show()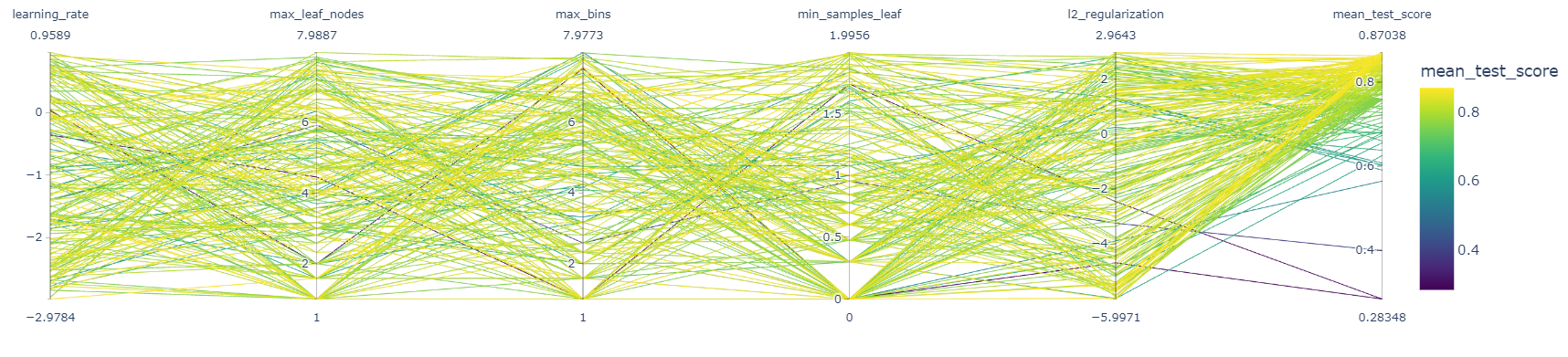
Transformamos la mayoría de los valores de los ejes tomando log10 o log2 para distribuir los rangos activos y mejorar la legibilidad del gráfico.
El gráfico de coordenadas paralelas muestra los valores de los hiperparámetros en diferentes columnas, mientras que la métrica de rendimiento está codificada por colores. Por tanto, somos capaces de inspeccionar rápidamente si existe un rango de hiperparámetros que funcionan o no.
Es posible seleccionar un rango de resultados haciendo clic y manteniendo presionado cualquier eje de coordenadas paralelas del gráfico. Luego podemos deslizar (mover) la selección del rango y cruzar dos selecciones para ver las interacciones. Podemos deshacer la selección haciendo clic una vez más en el mismo eje.
En particular para esta búsqueda de hiperparámetros, es interesante confirmar que las líneas amarillas (modelos de mejor rendimiento) alcanzan valores intermedios para la tasa de aprendizaje, es decir, valores entre las marcas -2 y 0 que corresponden a valores de tasa de aprendizaje de 0,01 y 1, una vez revertimos la transformación log10 para ese eje.
Pero ahora también podemos observar que no es posible seleccionar modelos de mayor rendimiento seleccionado líneas en el eje max_bins con valores de marcas entre 1 y 3.
Los otros hiperparámetros no son muy sensibles. Podemos comprobar que si seleccionamos en el eje learning_rate valores entre las marcas -1.5 y -0.5 y en el eje max_bins valores entre las marcas 5 y 8, siempre seleccionamos modelos con el mejor rendimiento, independientemente de los valores de los otros hiperparámetros.
Evaluación y ajuste de hiperparámetros
Hasta el momento hemosvisto dos enfoques para ajustar hiperparámetros. Sin embargo, no hemos presentado una forma apropiada para evaluar los modelos “tuneados”. En su lugar, nos hemos enfocado en el mecanismo usado para encontrar el mejor conjunto de hiperparámetros. Vamos a mostrar cómo evaluar modelos donde los hiperparámetros necesitan ser ajustados.
Partimos del mismo dataset, el cual hemos dividido en entrenamiento y prueba, y hemos realizado el mismo pipeline de preprocesado.
modelPipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education','marital-status','occupation', 'relationship','race', 'sex','native-country'])])),('classifier',HistGradientBoostingClassifier(max_leaf_nodes=4,random_state=42))])Please rerun this cell to show the HTML repr or trust the notebook.Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education','marital-status','occupation', 'relationship','race', 'sex','native-country'])])),('classifier',HistGradientBoostingClassifier(max_leaf_nodes=4,random_state=42))])ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education', 'marital-status','occupation', 'relationship', 'race', 'sex','native-country'])])['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']
OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=-1)
passthrough
HistGradientBoostingClassifier(max_leaf_nodes=4, random_state=42)
Evaluación sin ajuste de hiperparámetros
cv_results = cross_validate(model, X, y, cv=5)
cv_results = pd.DataFrame(cv_results)
cv_results| fit_time | score_time | test_score | |
|---|---|---|---|
| 0 | 0.527953 | 0.057048 | 0.863036 |
| 1 | 0.525952 | 0.051044 | 0.860784 |
| 2 | 0.545971 | 0.056046 | 0.860360 |
| 3 | 0.491422 | 0.052546 | 0.863124 |
| 4 | 0.495926 | 0.048542 | 0.867219 |
Las puntuaciones de validación cruzada provienen de 5-particiones. Entonces, podemos calcular la media y la desviación típica de la puntuación de generalización.
print(
f"Puntuación de generalización sin ajuste de hiperparámetros:\n"
f"{cv_results['test_score'].mean():.3f} +/- {cv_results['test_score'].std():.3f}"
)Puntuación de generalización sin ajuste de hiperparámetros:
0.863 +/- 0.003
Evaluación con ajuste de hiperparámetros
Vamos a presentar cómo evaluar el modelo con ajuste de hiperparámetros, lo que requiere un paso extra para seleccionar el mejor conjunto de parámetros. Ya vimos que podemos usar una estrategia de búsqueda que utiliza validación cruzada para encontrar el mejor conjunto de hiperparámetros. Aquí vamos a usar una estrategia de grid-search y reproduciremos los pasos que ya vimos anteriormente.
En primer lugar, vamos a incrustar nuestro modelo en un grid-search y especificar los parámetros y los valores de los parámetros que queremos explorar.
param_grid = {
'classifier__learning_rate': (0.05, 0.5),
'classifier__max_leaf_nodes': (10, 30),
}
model_grid_search = GridSearchCV(
model, param_grid=param_grid, n_jobs=-1, cv=2
)
model_grid_search.fit(X, y)GridSearchCV(cv=2,estimator=Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough',sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass','education','marital-status','occupation','relationship','race','sex','native-country'])])),('classifier',HistGradientBoostingClassifier(max_leaf_nodes=4,random_state=42))]),n_jobs=-1,param_grid={'classifier__learning_rate': (0.05, 0.5),'classifier__max_leaf_nodes': (10, 30)})Please rerun this cell to show the HTML repr or trust the notebook.GridSearchCV(cv=2,estimator=Pipeline(steps=[('preprocessor',ColumnTransformer(remainder='passthrough',sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass','education','marital-status','occupation','relationship','race','sex','native-country'])])),('classifier',HistGradientBoostingClassifier(max_leaf_nodes=4,random_state=42))]),n_jobs=-1,param_grid={'classifier__learning_rate': (0.05, 0.5),'classifier__max_leaf_nodes': (10, 30)})ColumnTransformer(remainder='passthrough', sparse_threshold=0,transformers=[('cat_preprocessor',OrdinalEncoder(handle_unknown='use_encoded_value',unknown_value=-1),['workclass', 'education', 'marital-status','occupation', 'relationship', 'race', 'sex','native-country'])])['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']
OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=-1)
passthrough
HistGradientBoostingClassifier(max_leaf_nodes=4, random_state=42)
Como vimos, cuando llamamos al método fit, el modelo embebido en grid-search es entrenado con cada una de las posibles combinaciones de parámetros resultado del cuadrante de parámetros. Se selecciona la mejor combinación, manteniendo aquella combinación que conduce a la mejor puntuación media de validación cruzada.
cv_results = pd.DataFrame(model_grid_search.cv_results_)
cv_results| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_classifier__learning_rate | param_classifier__max_leaf_nodes | params | split0_test_score | split1_test_score | mean_test_score | std_test_score | rank_test_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.603518 | 0.013511 | 0.260224 | 0.006005 | 0.05 | 10 | {'classifier__learning_rate': 0.05, 'classifie... | 0.863970 | 0.864707 | 0.864338 | 0.000369 | 4 |
| 1 | 0.898772 | 0.002502 | 0.319024 | 0.004754 | 0.05 | 30 | {'classifier__learning_rate': 0.05, 'classifie... | 0.871013 | 0.870317 | 0.870665 | 0.000348 | 1 |
| 2 | 0.300508 | 0.036280 | 0.163140 | 0.023520 | 0.5 | 10 | {'classifier__learning_rate': 0.5, 'classifier... | 0.866426 | 0.868679 | 0.867553 | 0.001126 | 2 |
| 3 | 0.261725 | 0.007006 | 0.152131 | 0.001501 | 0.5 | 30 | {'classifier__learning_rate': 0.5, 'classifier... | 0.867164 | 0.866836 | 0.867000 | 0.000164 | 3 |
model_grid_search.best_params_{'classifier__learning_rate': 0.05, 'classifier__max_leaf_nodes': 30}
Una importante advertencia aquí es la concerniente a la evaluación del rendimiento de generalización. De hecho, la media y la desviación típica de las puntuaciones calculadas por la validación cruzada en grid-search no son potencialmente buenas estimaciones del rendimiento de generalización que obtendríamos reentrenando un modelo con la mejor combinación de valores de hiperparámetros en el dataset completo. Hay que tener en cuenta que scikit-learn, por defecto, ejecuta automáticamente este reentreno cuando llamamos a model_grid_search.fit. Este modelo reentrenado se entrena con más datos que los diferentes modelos entrenados internamente durante la validación cruzada de grid-search.
Por lo tanto, usamos el conocimiento del dataset completo para decidir los hiperparámetros de nuestro modelo y entrenar el modelo reajustado. Debido a esto, se debe mantener un conjunto de prueba externo para la evaluación final del modelo reajustado. Destacamos aquí el proceso usando una única división entrenamiento-prueba.
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
model_grid_search.fit(X_train, y_train)
accuracy = model_grid_search.score(X_test, y_test)
print(f"Precisión en el conjunto de prueba: {accuracy:.3f}")Precisión en el conjunto de prueba: 0.879
La medida de puntuación en el conjunto de prueba final está casi en el mismo rango que la puntuación de validación cruzada interna para la mejor combinación de hiperparámetros. Esto es tranquilizador, ya que significa que el procedimiento de ajuste no ha provocado un overfitting significativo en sí mismo (de lo contrario, la puntuación de prueba final habría sido más baja que la puntuación de validación cruzada interna). Eso era de esperar porque nuestro grid-search exploró muy pocas combinaciones de hiperparámetros en aras de la velocidad. La puntuación de prueba del modelo final es realmente un poco más alta de la que cabría esperar de la validación cruzada interna. Esto también era de esperar porque el modelo reajustado se entrena en un dataset más grande que los modelos evaluados en el bucle de validación cruzada interno del procedimiento de grid-search. Este suele ser el caso de los modelos entrenados con un gran número de instancias, tienden a generalizar mejor.
En el código anterior, la selección de los mejores hiperparámetros se realizó únicamente en el conjunto de entrenamiento de la división inicial entrenamiento-prueba. Después, evaluamos el rendimiento de generalización de nuestro modelo tuneado en el conjunto de prueba restante. Esto se puede mostrar esquemáticamente en el siguiente diagrama:
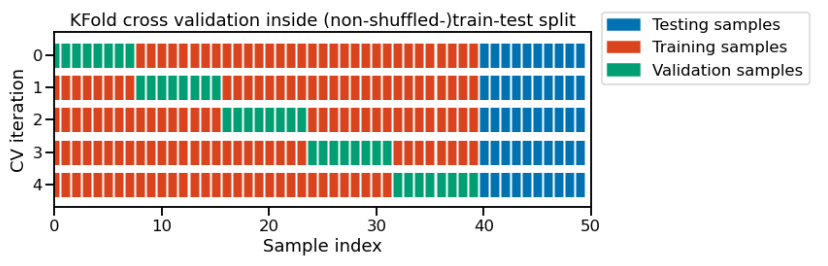
Esta figura muestra el caso particular de la estrategia de validación cruzada de K-particiones usando n_splits=5 para dividir el conjunto de entrenamiento proveniente de la división entrenamient-prueba. Para cada división de validación cruzada, el procedimiento entrena un modelo en todas las instancias rojas, evalúa la puntuación de un conjunto dado de hiperparámetros en las instancias verdes. Los mejores hiperparámetros se seleccionan basándose en estas puntuaciones intermedias. El modelo final tuneado con esos hiperparámetros se entrena en la concatenación de instancias rojas y verdes y se evalúa en las instancias azules.
Las instancias verdes a menudo se denominan conjuntos de validación para diferenciarlos del conjunto de prueba final en azul.
Sin embargo, esta evaluación solo nos proporciona una estimación puntual única del rendimiento de generalización. Como recordamos al principio, es beneficioso disponer de una idea aproximada de la incertidumbre de nuestro rendimiento de generalización estimado. Por lo tanto, deberíamos usar adicionalmente una validación cruzada para esta estimación.
Este patrón se denomina validación-cruzada anidada. Usamos la validación cruzada interna para la selección de los hiperparámetros y la validación cruzada externa para la evaluación del rendimiento de generalización del modelo tuneado reajustado.
En la práctica, solo necesitamos incrustar grid-search en la función cross-validate para ejecutar dicha evaluación.
cv_results = cross_validate(
model_grid_search, X, y, cv=5, n_jobs=-1, return_estimator=True
)cv_results = pd.DataFrame(cv_results)
cv_test_scores = cv_results["test_score"]
print(
"Puntuación de generalización con ajuste de hiperparámetros:\n"
f"{cv_test_scores.mean():.3f} +/- {cv_test_scores.std():.3f}"
)Puntuación de generalización con ajuste de hiperparámetros:
0.871 +/- 0.003
Este resultado es compatible con la puntuación de prueba medida en la división externa entrenamiento-prueba. Sin embargo, en este caso obtenemos conocimiento sobre la variablidad de nuestra estimación del rendimiento de generalización gracias a la medida de la desviación típica de las puntuaciones medidas en la validación cruzada externa.
A continuación se muestra una representación esquemática del procedimiento completo de validación cruzada anidada.
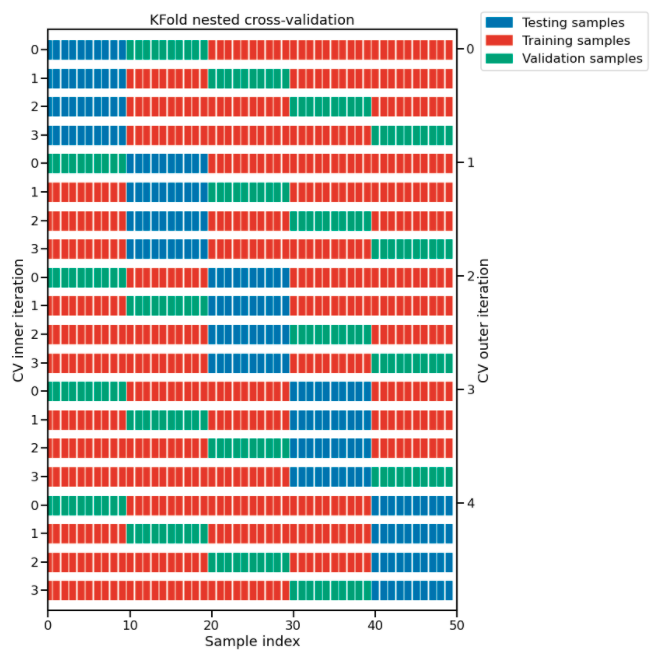
En la figura se ilustra la estrategia de validación cruzada anidada usando cv_inner = Kfold(n_splits=4) y cv_outer = Kfold(n_splits=5).
Para cada división de validación cruzada interna (indexada en la parte izquierda), el procedimiento entrena un modelo en todas las muestras rojas y evalúa la calidad de los hiperparámetros en las muestras verdes.
Para cada división de validación cruzada externa (indexada en la parte derecha), se seleccionan los mejores hiperparámetros basándose en las puntuaciones de validación (calculadas en las muestras verdes) y se reajusta un modelo en la concatenación de las instancias rojas y verdes para esa iteración de validación cruzada externa.
El rendimiento de generalización de los 5 modelos reajustados del bucle de validación cruzada externa se evalúa en las instancias azules para obtener las puntuaciones finales.
Pasando el parámetro return_estimator=True podemos comprobar el valor de los mejores hiperparámetros obtenidos para cada partición de la validación cruzada externa.
for cv_fold, estimator_in_fold in enumerate(cv_results["estimator"]):
print(
f"Mejores hiperparámetros para la partición nº{cv_fold+1}:\n"
f"{estimator_in_fold.best_params_}"
)Mejores hiperparámetros para la partición nº1:
{'classifier__learning_rate': 0.05, 'classifier__max_leaf_nodes': 30}
Mejores hiperparámetros para la partición nº2:
{'classifier__learning_rate': 0.05, 'classifier__max_leaf_nodes': 30}
Mejores hiperparámetros para la partición nº3:
{'classifier__learning_rate': 0.05, 'classifier__max_leaf_nodes': 30}
Mejores hiperparámetros para la partición nº4:
{'classifier__learning_rate': 0.5, 'classifier__max_leaf_nodes': 10}
Mejores hiperparámetros para la partición nº5:
{'classifier__learning_rate': 0.05, 'classifier__max_leaf_nodes': 30}
Es interesante ver si el procedimiento de ajuste de hiperparámetros siempre selecciona valores similares para los hiperparámetros. Si es el caso, entonces todo está bien. Significa que podemos desplegar un modelo ajustado con esos hiperparámetros y esperar que tenga un rendimiento predictivo real cercano al que medimos en la validación cruzada externa.
Pero también es posible que algunos hiperparámetros no tengan ninguna importancia y, como resultado de diferentes sesiones de ajuste, den resultados diferentes. En este caso, servirá cualquier valor. Normalmente esto se puede confirmar haciendo un gráfico de coordenadas paralelas de los resultados de una gran búsqueda de hiperparáemtros, como ya vimos.
Desde el punto de vista de la implementación, se podría optar por implementar todos los modelos encontrados en el ciclo de validación cruzada externa y votar para obtener las predicciones finales. Sin embargo, esto puede causar problemas operativos debido a que usa más memoria y hace que la predicción sea más lenta, lo que resulta en un mayor uso de recursos computacionales por predicción.
Resumen
-
Los hiperparámetros tienen un impacto en el rendimiento de los modelos y deben ser elegirse sabiamente;
-
La búsqueda de los mejores hiperparámetros se puede automatizar con un enfoque de grid-search o búsqueda automática;
-
Grid-search es costoso y no escala cuando el número de hiperparámetros a optimizar incrementa. Además, la combinación se muestrea únicamente en una retícula regular.
-
Una búsqueda aleatoria permite buscar con una propuesta fija incluso con un número creciente de hiperparámetros. Además, la combinación se muestrea en una retícula no regular.
-
El overfitting es causado por el tamaño limitado del conjunto de entrenamiento, el ruido en los datos y la alta flexibilidad de los modelos de machine learning comunes.
-
El underfitting sucede cuando las funciones de predicción aprendidas sufren de errores sistemáticos. Esto se puede producir por la elección de la familia del modelo y los parámetros, lo cuales conducen a una carencia de flexibilidad para capturar la estructura repetible del verdadero proceso de generación de datos.
-
Para un conjunto de entrenamiento dado, el objetivo es minimizar el error de preba ajustando la familia del modelo y sus parámetros para encontrar el mejor equilibrio entre overfitting y underfitting.
-
Para una familia de modelo y parámetros dados, incrementar el tamaño del conjunto de entrenamiento disminuirá el overfitting, pero puede causar un incremento del underfitting.
-
El error de prueba de un modelo que no tiene overfitting ni underfitting puede ser alto todavía si las variaciones de la variable objetivo no pueden ser determinadas completamente por las variables de entrada. Este error irreductible es causado por lo que algunas veces llamamos error de etiqueta. En la práctica, esto sucede a menudo cuando por una razón u otra no tenemos acceso a features importantes.
Algunas referencias a seguir con ejemplos de algunos conceptos mencionados: